MATHEMINUTES
"Interesting aspects of mathematics in bitesize chunks"
Autograph excercises from OWEN ELTON
Complex adventures in Autograph - 1
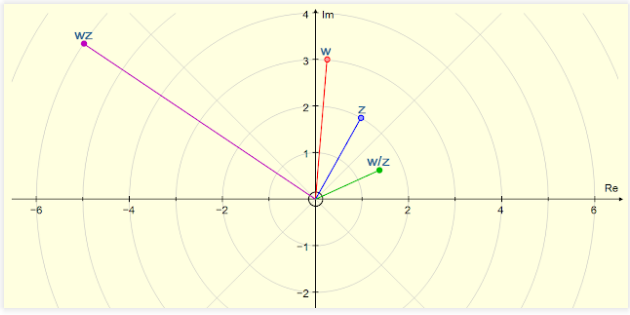
The graphical representation of complex numbers is an essential tool in understanding their behaviour; the underlying algebra can be very fiddly unless you have a useful picture in your mind or, even better, scribbled on paper or, better still, interactive on a screen. The new complex plane in Autograph 4 not only makes aspects of A level further maths clearer but can illustrate (as in the picture above) some of the complex analysis one might encounter on a maths degree.
Autograph - 2
Complex adventures in Autograph - 2
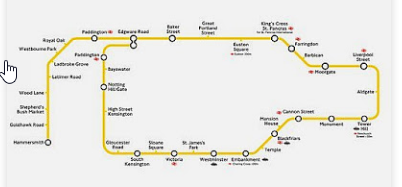
Last time, we began to explore some of the new complex features of Autograph 4 and I suggested that next I'd demonstrate some complex transformations. Assuming not everyone reading this has a background in complex analysis, however, I think a brief intermezzo is in order. First you need to understand what is meant by a circline . . .
Autograph - 3
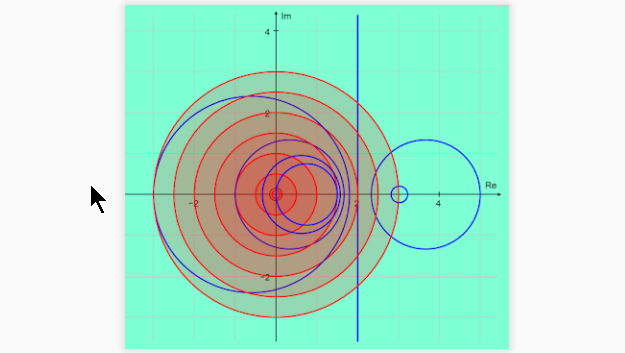
Complex adventures in Autograph - 3
Maths blogs are not renowned for lengthy cliffhangers but I may inadvertently have managed one a couple of months ago. A pair of posts on the new features of Autograph 4 ended in a discussion of circlines and the promise of exploring some complex transformations.
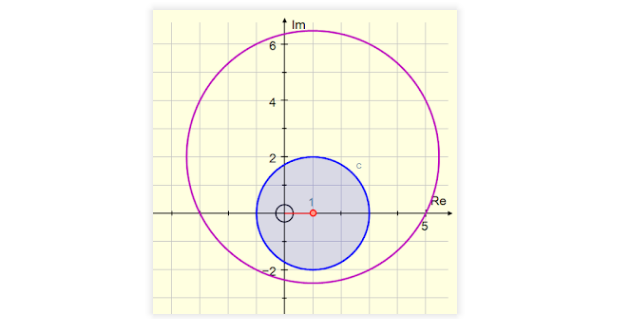
Autograph - 4
Complex adventures in Autograph - 4
Earlier in the year I wrote a few posts about the complex plane feature in Autograph 4. First, I explored some complex arithmetic, then investigated the idea of a circline (either a circle or a line) before seeing how we might transform them. To wrap these up, it is well worth mentioning the incredible control we can have over transformations between circlines, thanks to a map named after August Möbius - a man more famous for his strip.
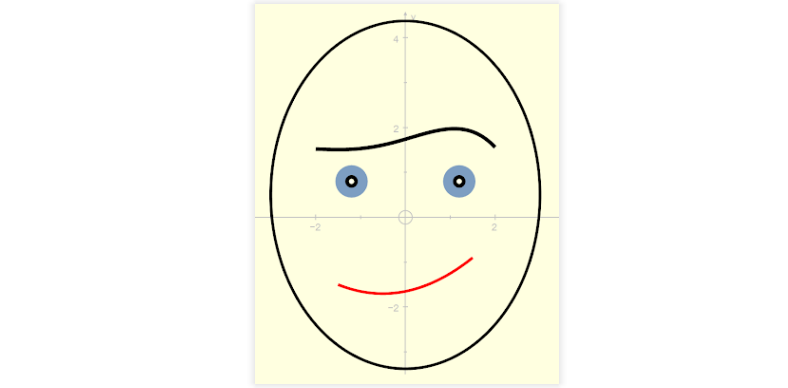
The Many and Varied Expressions of Monobrow Man
He has a quadratic mouth and a quartic monobrow. You can manipulate his expression in this Autograph Activities page. You might also learn a bit about the affect of changing the coefficients of polynomials on their related curves.
Here are a couple of examples of the faces that Monobrow Man can pull. What can you come up with?
Eggquations
As you tuck into your chocolate eggs tomorrow will you, at any stage, wonder how you might model their shape? Well one man who has is Nobuo Yamamoto of Japan's TDDC Lab. On his webpage he has written seven different articles about equations of eggs. They make fascinating reading; I will share with you his first suggestion which results in the following shape (seen here from four different angles):

Porto's Hyperbolic Slit
There were some things I had expected from a brief half-term visit to Porto. They largely involved wine (fortified), Portuguese tarts (custard), and a little mathematics
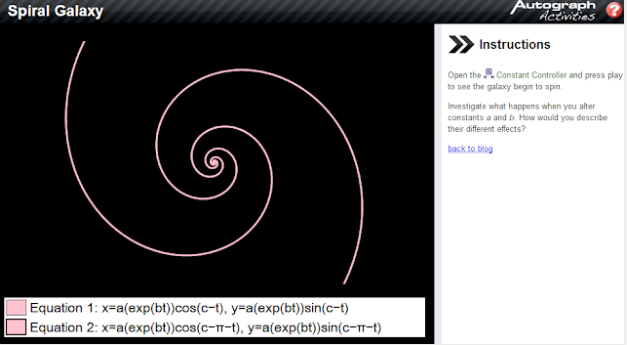
A Galaxy Far Away
A couple of days ago, I read that astronomers had discovered the largest spiral galaxy known to humankind. It is called NGC 6872 and lies a mind-boggling 212 million light-years away. The gargantuan object contains many infant stars, born as a result of a "recent" collision with another galaxy (IC 4970) about 130 million years ago. This figure doesn't seem correct, however; if it was, we would only receive information about the collision in 82 million years' time, so I presume the journalist means 212+130 million years ago - these intergalactic distances can be a right thorn in simultaneity's back!